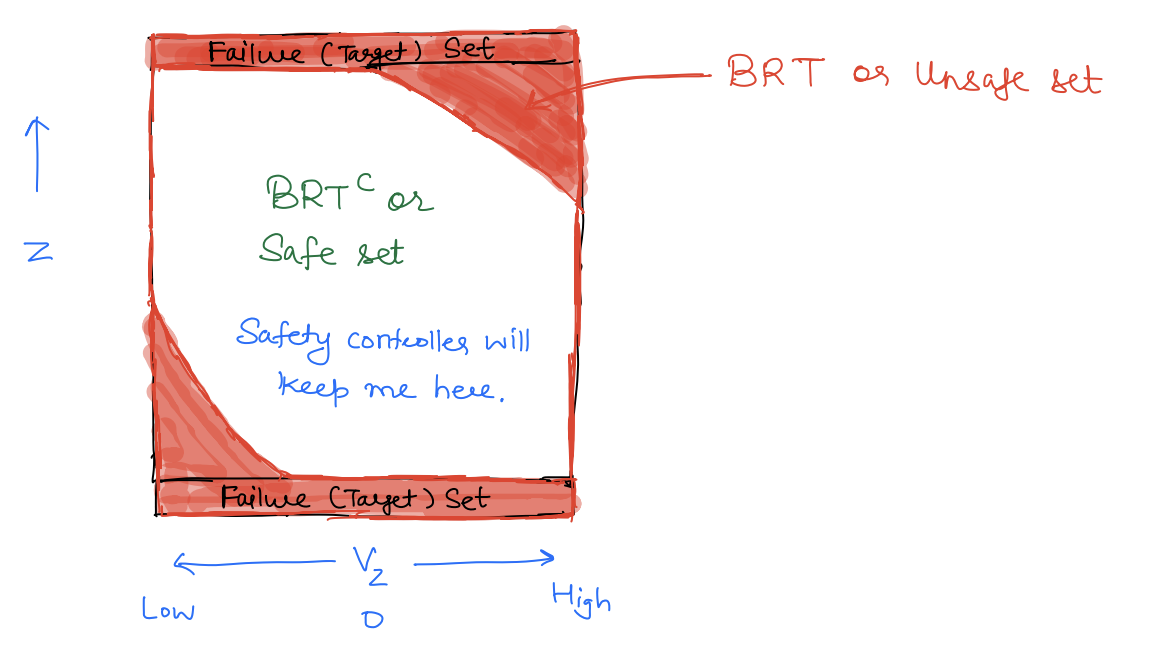
Safe Control So far, we have seen how HJI-VI can be used to compute the B R T ( t ) B R T(t) BRT ( t ) B R T C ( t ) {BRT}^{C}(t) BRT C ( t )
To derive a safety controller, let's go back to the discrete-time DP where the value function is defined by the Bellman equation:
V ( x , t ) = max u { L ( x , u ) + V ( x + , t + 1 ) } V(x, t)=\max _{u}\left\{L(x, u)+V\left(x_{+}, t+1\right)\right\} V ( x , t ) = u max { L ( x , u ) + V ( x + , t + 1 ) } Here, the optimal controller at state x x x t t t
u ∗ ( x , t ) = arg max u { L ( x , u ) + V ( x + , t + 1 ) } u^{*}(x, t)=\argmax_{u}\left\{L(x, u)+V\left(x_{+}, t+1\right)\right\} u ∗ ( x , t ) = u arg max { L ( x , u ) + V ( x + , t + 1 ) } Indeed if I follow this optimal control sequence starting from state x x x t t t V ( x , t ) V(x, t) V ( x , t )
In other words, u ∗ ( x , ⋅ ) u^{*}\left(x, \cdot\right) u ∗ ( x , ⋅ ) V ( x , t ) V(x, t) V ( x , t )
Similarly, in continuous time, the Bellman equation is replaced by HJB PDE:
∂ V ∂ t + max u { L ( x , u ) + ∂ V ∂ x ⋅ f ( x , u ) } = 0 \frac{\partial V}{\partial t}+\max _{u}\left\{L(x, u)+\frac{\partial V}{\partial x} \cdot f(x, u)\right\}=0 ∂ t ∂ V + u max { L ( x , u ) + ∂ x ∂ V ⋅ f ( x , u ) } = 0 Here also the optimal control u ∗ ( x , t ) u^{*}\left(x, t\right) u ∗ ( x , t ) V ( x , t ) V\left(x, t\right) V ( x , t )
u ∗ ( x , t ) = arg max u { L ( x , u ) + ∂ V ∂ x ( x , t ) ⋅ f ( x , u ) } u^{*}(x, t)=\argmax_{u}\left\{L(x, u)+\frac{\partial V}{\partial x}(x, t) \cdot f(x, u)\right\} u ∗ ( x , t ) = u arg max { L ( x , u ) + ∂ x ∂ V ( x , t ) ⋅ f ( x , u ) } The same principle applies in the context of reachability. If we are outside the unsafe set (ie. V ( x , t ) > 0 V(x, t)>0 V ( x , t ) > 0 [ t , T ] [t, T] [ t , T ]
min { l ( x ) − V ( x , t ) , ∂ V ∂ t + max u ∂ V ∂ x ⋅ f ( x , u ) } = 0 V ( x , T ) = l ( x ) \begin{gathered} \min \left\{l(x)-V(x, t), \frac{\partial V}{\partial t}+\max _{u} \frac{\partial V}{\partial x} \cdot f(x, u)\right\}=0 \\ V(x, T)=l(x) \end{gathered} min { l ( x ) − V ( x , t ) , ∂ t ∂ V + u max ∂ x ∂ V ⋅ f ( x , u ) } = 0 V ( x , T ) = l ( x ) The optimal control that the system can apply to maximize the signed distance to L \mathcal{L} L
u safe ∗ ( x , t ) = arg max u ∂ V ( x , t ) ∂ x ⋅ f ( x , u ) u_{\text{safe}}^{*}(x, t)=\argmax_{u} \frac{\partial V(x, t)}{\partial x} \cdot f(x, u) u safe ∗ ( x , t ) = u arg max ∂ x ∂ V ( x , t ) ⋅ f ( x , u ) In the cases where the BRT converges, we can ignore the time argument. Letting V ∗ ( x ) V^{*}(x) V ∗ ( x )
u safe ∗ ( x ) = arg max u ∂ V ∗ ( x ) ∂ x ⋅ f ( x , u ) u_{\text{safe}}^{*}(x)=\argmax_u \frac{\partial V^{*}(x)}{\partial x} \cdot f(x, u) u safe ∗ ( x ) = u arg max ∂ x ∂ V ∗ ( x ) ⋅ f ( x , u ) Intuitively, u ∗ u^{*} u ∗ V V V u safe ∗ ( x ) u_{\text{safe}}^{*}(x) u safe ∗ ( x ) x x x
If the system starts outside the BRT and applies u safe ∗ ( x ) u_{\text{safe}}^{*}(x) u safe ∗ ( x )
It is particularly easy to compute this safe control for control-affine systems dynamics. For such systems, the dynamics can be written as f ( x , u ) = f 1 ( x ) + f 2 ( x ) u ← f(x, u)=f_{1}(x)+f_{2}(x) u \leftarrow f ( x , u ) = f 1 ( x ) + f 2 ( x ) u ←
Thus,
∂ V ∗ ( x ) ∂ x ⋅ f ( x , u ) = ∂ V ∗ ∂ x ⋅ f 1 ( x ) + ∂ V ∗ ∂ x ⋅ f 2 ( x ) u \frac{\partial V^{*}(x)}{\partial x} \cdot f(x, u)=\frac{\partial V^{*}}{\partial x} \cdot f_{1}(x)+\frac{\partial V^{*}}{\partial x} \cdot f_{2}(x) u ∂ x ∂ V ∗ ( x ) ⋅ f ( x , u ) = ∂ x ∂ V ∗ ⋅ f 1 ( x ) + ∂ x ∂ V ∗ ⋅ f 2 ( x ) u u safe ∗ ( x ) = argmax u ∂ V ∗ ∂ x ⋅ f 1 ( x ) + ∂ V ∗ ∂ x ⋅ f 2 ( x ) u = argmax u ∂ V ∗ ∂ x ⋅ f 2 ( x ) u u_{\text {safe }}^{*}(x)=\underset{u}{\operatorname{argmax}} \frac{\partial V^{*}}{\partial x} \cdot f_{1}(x)+\frac{\partial V^{*}}{\partial x} \cdot f_{2}(x) u=\underset{u}{\operatorname{argmax}} \frac{\partial V^{*}}{\partial x} \cdot f_{2}(x) u u safe ∗ ( x ) = u argmax ∂ x ∂ V ∗ ⋅ f 1 ( x ) + ∂ x ∂ V ∗ ⋅ f 2 ( x ) u = u argmax ∂ x ∂ V ∗ ⋅ f 2 ( x ) u This is a linear objective function in u u u
Example: A Longitudinal Quadrotor The system state is given as x = [ z v ] x=\left[\begin{array}{l}z \\ v\end{array}\right] x = [ z v ] z ˙ = v v ˙ = k u + g \quad \begin{aligned} & \dot{z}=v \\ & \dot{v}=k u+g\end{aligned} z ˙ = v v ˙ = k u + g
Moreover let ∣ u ∣ ≤ u ⃗ |u| \leq \vec{u} ∣ u ∣ ≤ u
In this case, f ( x , u ) = [ v k u + g ] = [ v g ] + [ 0 k ] u f(x, u)=\left[\begin{array}{c}v \\ k u+g\end{array}\right] =\left[\begin{array}{l}v \\ g\end{array}\right]+\left[\begin{array}{l}0 \\ k\end{array}\right] u f ( x , u ) = [ v k u + g ] = [ v g ] + [ 0 k ] u
Thus, u safe ∗ = arg max u ∂ v ∗ ∂ x ⋅ f ( x , u ) u_{\text {safe}}^{*}=\argmax_u \frac{\partial v^{*}}{\partial x} \cdot f(x, u) u safe ∗ = arg max u ∂ x ∂ v ∗ ⋅ f ( x , u )
Let ∂ V ∗ ∂ x = [ p 1 ( x ) p 2 ( x ) ] ⇒ ∂ V ∗ ∂ x ⋅ f ( x , u ) = [ p 1 ( x ) p 2 ( x ) ] ( [ v g ] + [ 0 k ] ) \frac{\partial V^{*}}{\partial x}=\left[\begin{array}{ll}p_{1}(x) & p_{2}(x)\end{array}\right] \Rightarrow \frac{\partial V^{*}}{\partial x} \cdot f(x, u)=\left[\begin{array}{ll}p_{1}(x) & p_{2}(x)\end{array}\right]\left(\left[\begin{array}{l}v \\ g\end{array}\right]+\left[\begin{array}{l}0 \\ k\end{array}\right]\right) ∂ x ∂ V ∗ = [ p 1 ( x ) p 2 ( x ) ] ⇒ ∂ x ∂ V ∗ ⋅ f ( x , u ) = [ p 1 ( x ) p 2 ( x ) ] ( [ v g ] + [ 0 k ] )
∂ v ∗ ∂ x ⋅ f ( x , u ) = ( p 1 ( x ) v + p 2 ( x ) g ) + ( p 2 ( x ) k ) u ← \frac{\partial v^{*}}{\partial x} \cdot f(x, u)=\left(p_{1}(x) v+p_{2}(x) g\right)+\left(p_{2}(x) k\right) u \leftarrow ∂ x ∂ v ∗ ⋅ f ( x , u ) = ( p 1 ( x ) v + p 2 ( x ) g ) + ( p 2 ( x ) k ) u ← u u u
u safe ∗ ( x ) = arg max ∣ u ∣ ⩽ u ˉ ( p 1 ( x ) v + p 2 ( x ) g ) + ( b 2 ( x ) k ) u = { u ˉ if p 2 ( x ) ⩾ 0 − u ˉ if p 2 ( x ) < 0 \begin{aligned} u_{\text {safe}}^{*}(x)&=\argmax_{|u| \leqslant \bar{u}}\left(p_{1}(x) v+p_{2}(x) g\right)+\left(b_{2}(x) k\right) u \\ &=\left\{\begin{array}{c} \bar{u} \quad \text { if } \; p_{2}(x) \geqslant 0 \\ -\bar{u} \quad \text { if } \; p_{2}(x)<0 \end{array}\right. \end{aligned} u safe ∗ ( x ) = ∣ u ∣ ⩽ u ˉ arg max ( p 1 ( x ) v + p 2 ( x ) g ) + ( b 2 ( x ) k ) u = { u ˉ if p 2 ( x ) ⩾ 0 − u ˉ if p 2 ( x ) < 0 → \rightarrow →
Example: Planar Car State: [ p x b y θ ] \left[\begin{array}{l}p_{x} \\ b_{y} \\ \theta\end{array}\right] ⎣ ⎡ p x b y θ ⎦ ⎤ f ( x , u ) = [ v cos θ v sin θ ω ] f(x, u)=\left[\begin{array}{c}v \cos \theta \\ v \sin \theta \\ \omega\end{array}\right] f ( x , u ) = ⎣ ⎡ v cos θ v sin θ ω ⎦ ⎤
System control: ω \omega ω ∣ ω ∣ ⩽ ω ˉ |\omega| \leqslant \bar{\omega} ∣ ω ∣ ⩽ ω ˉ
Once again, we have a control affine system
f ( x , u ) = [ v cos θ v sin θ 0 ] + [ 0 0 1 ] u u safe ∗ = arg max u ∂ V ∗ ∂ x ⋅ ( f 1 ( x ) + f 2 ( x ) u ) = arg max u [ p 1 ( x ) p 2 ( x ) p 3 ( x ) ] f 2 ( x ) u = agmax p 3 ( x ) u = { ω ˉ if p 3 ( x ) ⩾ 0 − ω ˉ if p 3 ( x ) < 0 \begin{aligned} f(x, u)&=\left[\begin{array}{c} v \cos \theta \\ v \sin \theta \\ 0 \end{array}\right]+\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right] u \\ u_{\text {safe }}^{*}&=\argmax_{u} \frac{\partial V^{*}}{\partial x} \cdot\left(f_{1}(x)+f_{2}(x) u\right) \\ & =\argmax_u \left[p_{1}(x) \quad p_{2}(x) \quad p_{3}(x)\right] f_{2}(x) u \\ & = \operatorname{agmax} p_{3}(x) u \\ & =\left\{\begin{array}{l} \bar{\omega} \quad \text { if } \; p_{3}(x) \geqslant 0 \\ -\bar{\omega} \quad \text { if } \; p_{3}(x)<0 \end{array}\right. \end{aligned} f ( x , u ) u safe ∗ = ⎣ ⎡ v cos θ v sin θ 0 ⎦ ⎤ + ⎣ ⎡ 0 0 1 ⎦ ⎤ u = u arg max ∂ x ∂ V ∗ ⋅ ( f 1 ( x ) + f 2 ( x ) u ) = u arg max [ p 1 ( x ) p 2 ( x ) p 3 ( x ) ] f 2 ( x ) u = agmax p 3 ( x ) u = { ω ˉ if p 3 ( x ) ⩾ 0 − ω ˉ if p 3 ( x ) < 0 Example: Non-control-affine Sometimes even when the system is not control-affine we can compute the safety control law. For example, consider the following 2D human dynamics model:
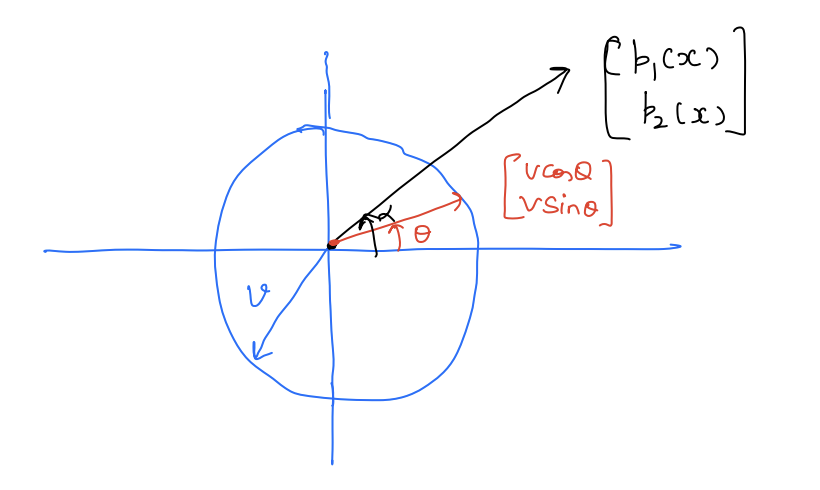
x = [ p x b y ] with f ( x , u ) = [ v cos θ v sin θ ] x=\left[\begin{array}{l} p_{x} \\ b_{y} \end{array}\right] \text { with } f(x, u)=\left[\begin{array}{l} v \cos \theta \\ v \sin \theta \end{array}\right] x = [ p x b y ] with f ( x , u ) = [ v cos θ v sin θ ] Here, u = θ u=\theta u = θ θ \theta θ
u safe ∗ ( x ) = arg max u [ p 1 ( x ) p 2 ( x ) ] [ v cos θ v sin θ ] u_{\text {safe }}^{*}(x)=\argmax_u \left[\begin{array}{ll} p_{1}(x) & p_{2}(x) \end{array}\right]\left[\begin{array}{c} v \cos \theta \\ v \sin \theta \end{array}\right] u safe ∗ ( x ) = u arg max [ p 1 ( x ) p 2 ( x ) ] [ v cos θ v sin θ ] The above objective is a dot product between two vectors. Pictorially:
If we want to maximize the dot product, we should pick θ = α \theta=\alpha θ = α u safe ∗ ( x ) = α ( x ) u_{\text {safe}}^{*}(x)=\alpha(x) u safe ∗ ( x ) = α ( x ) α ( x ) = tan − 1 ( p 2 ( x ) p 1 ( x ) ) \alpha(x)=\tan ^{-1}\left(\frac{p_{2}(x)}{p_{1}(x)}\right) α ( x ) = tan − 1 ( p 1 ( x ) p 2 ( x ) )
Safety Filtering Often in robotic systems, we not only care about safety but also care about achieving a performance objective. After all, a self-driving car is safe if it doesn't move at all, but such a case is hard of any use from a practical viewpoint. In such cases, it is important to maintain performance while ensuring safety. One way to do so is via safety filtering.
The idea of safety filtering is to continue to apply a nominal performance controller (computed via MPC, RL, or even PID controller) until the safety is at risk; otherwise, apply a safety controller.
Let u norm ( x ) u_{\text{norm}}(x) u norm ( x ) x x x u norm ( x ) u_{\text{norm}}(x) u norm ( x )
u ∗ ( x ) = { u norm ( x ) if system is safe u safe ∗ ( x ) if safety at risk u^{*}(x)= \begin{cases}u_{\text {norm}}(x) & \text { if system is safe } \\ u_{\text {safe}}^{*}(x) & \text { if safety at risk }\end{cases} u ∗ ( x ) = { u norm ( x ) u safe ∗ ( x ) if system is safe if safety at risk But how do we know when safety is at risk? Well, we know the system is safe as long as it is outside the unsafe set. Thus,
u x ( x ) = { u norm ( x ) if V x ( x ) > 0 u safe x ( x ) if V x ( x ) = 0 (A) u^{x}(x)= \begin{cases}u_{\text{norm}}(x) & \text { if } V^{x}(x)>0 \\ u_{\text {safe }}^{x}(x) & \text { if } V^{x}(x)=0 \end{cases} \tag{A} u x ( x ) = { u norm ( x ) u safe x ( x ) if V x ( x ) > 0 if V x ( x ) = 0 ( A ) The control law in A is called least-restrictive safety filtering because it minimally interferes with the performance controller and only overrides it when the system safety is at risk.
The problem with the control law in (A) is that it leads to a sudden switch in the control policy near the boundary of the unsafe set which might deviate significantly from the nominal controller. Moreover, it is sufficient to apply any safe controller and not necessarily the one that maximizes the value function. Thus, we can devise an alternative safety filtering lave as follows:
u ∗ ( x ) = arg min u ∥ u − u norm ∥ 2 2 s.t. u is safe } Remain as close to u norm as possible while maintaining safety \left.\begin{array}{rl} u^{*}(x)=& \argmin_u\left\|u-u_{\text {norm}}\right\|_{2}^{2} \\ & \text { s.t. } u \text { is safe } \end{array}\right\} \begin{aligned} & \text {Remain as close to } \\ & u_{\text {norm}} \text{ as possible } \\ & \text {while maintaining safety } \end{aligned} u ∗ ( x ) = arg min u ∥ u − u norm ∥ 2 2 s.t. u is safe } Remain as close to u norm as possible while maintaining safety But how do we obtain the set of all safe controls?
u u u ≡ V ∗ ( x ( t + δ ) ) ⩾ 0 \equiv V^{*}(x(t+\delta)) \geqslant 0 ≡ V ∗ ( x ( t + δ )) ⩾ 0 δ \delta δ u u u
V ∗ ( x ( t + δ ) ) ≈ V ∗ ( x ) + δ ∂ V ∗ ∂ x ⋅ f ( x , u ) ≥ 0 V^{*}(x(t+\delta)) \approx V^{*}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f(x, u) \geq 0 V ∗ ( x ( t + δ )) ≈ V ∗ ( x ) + δ ∂ x ∂ V ∗ ⋅ f ( x , u ) ≥ 0 ⇒ u ∗ ( x ) = arg min u ∥ u − u norm ∥ 2 2 s.t. V ∗ ( x ) + δ ∂ V x ∂ x ⋅ f ( x , u ) ⩾ 0 \begin{aligned} \Rightarrow u^{*}(x)= & \argmin_u \left\|u-u_{\text {norm}}\right\|_{2}^{2} \\ & \text { s.t. } V^{*}(x)+\delta \frac{\partial V^{x}}{\partial x} \cdot f(x, u) \geqslant 0 \end{aligned} ⇒ u ∗ ( x ) = u arg min ∥ u − u norm ∥ 2 2 s.t. V ∗ ( x ) + δ ∂ x ∂ V x ⋅ f ( x , u ) ⩾ 0 For a control affine system:
f ( x , u ) = f 1 ( x ) + f 2 ( x ) u f\left(x, u\right)=f_{1}(x)+f_{2}(x) u f ( x , u ) = f 1 ( x ) + f 2 ( x ) u Thus, the constraint can be re-written as:
V ∗ ( x ) + δ ∂ V ∗ ∂ x ⋅ f 1 ( x ) + δ ∂ V ∗ ∂ x ⋅ f 2 ( x ) u ⩾ 0 V^{*}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{1}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{2}(x) u \geqslant 0 V ∗ ( x ) + δ ∂ x ∂ V ∗ ⋅ f 1 ( x ) + δ ∂ x ∂ V ∗ ⋅ f 2 ( x ) u ⩾ 0 Since we know x x x V ∗ V^{*} V ∗ u u u A u + b ⩾ 0 A u+b \geqslant 0 A u + b ⩾ 0
A = δ ∂ V ∗ ∂ x ⋅ f 2 ( x ) b = V ∗ ( x ) + δ ∂ V ∗ ∂ x ⋅ f 1 ( x ) \begin{aligned} A&=\delta \frac{\partial V^{*}}{\partial x} \cdot f_{2}(x) \\ b&=V^{*}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{1}(x) \end{aligned} A b = δ ∂ x ∂ V ∗ ⋅ f 2 ( x ) = V ∗ ( x ) + δ ∂ x ∂ V ∗ ⋅ f 1 ( x ) Thus, the safety filtering law can be written as:
u ∗ ( x ) = arg min u ∥ u − u norm ∥ 2 2 s.t. A u + b ⩾ 0 (B) \begin{aligned} u^{*}(x)=&\argmin_u \left\|u-u_{\text {norm}}\right\|_{2}^{2} \\ & \text { s.t. } A u+b \geqslant 0 \end{aligned} \tag{B} u ∗ ( x ) = u arg min ∥ u − u norm ∥ 2 2 s.t. A u + b ⩾ 0 ( B ) The safety filtering law in (B) is a QP-based law and is quite popular in robotics. because it can be efficiently solved online.
Note that people use a variety of cost functions, including ∥ u ∥ 2 \|u\|^{2} ∥ u ∥ 2 ∥ u − u last ∥ 2 2 \left\|u-u_{\text {last}}\right\|_{2}^{2} ∥ u − u last ∥ 2 2 Example: Longitudinal Quadrotor f ( x ) = [ v g ] + [ 0 k ] u and let ∂ v ∗ ∂ x ( x ) = [ p 1 ( x ) p 2 ( x ) ] as before. A = δ [ p 1 ( x ) p 2 ( x ) ] [ 0 k ] u = δ p 2 ( x ) k u b = V ∗ ( x ) + δ p 1 ( x ) v + δ p 2 ( x ) g \begin{aligned} & f(x)=\left[\begin{array}{l} v \\ g \end{array}\right]+\left[\begin{array}{l} 0 \\ k \end{array}\right] u \quad \text { and let } \frac{\partial v^{*}}{\partial x}(x)=\left[p_{1}(x) \quad p_{2}(x)\right] \text { as before. } \\ & A=\delta\left[p_{1}(x) \quad p_{2}(x)\right]\left[\begin{array}{l} 0 \\ k \end{array}\right] u=\delta p_{2}(x) k u \\ & b=V^{*}(x)+\delta p_{1}(x) v+\delta p_{2}(x) g \end{aligned} f ( x ) = [ v g ] + [ 0 k ] u and let ∂ x ∂ v ∗ ( x ) = [ p 1 ( x ) p 2 ( x ) ] as before. A = δ [ p 1 ( x ) p 2 ( x ) ] [ 0 k ] u = δ p 2 ( x ) k u b = V ∗ ( x ) + δ p 1 ( x ) v + δ p 2 ( x ) g QP problem that needs to be solved at x x x
min u ∥ u − u norm ∥ 2 s.t. ( δ p 2 ( x ) k ) u ≤ ( V ∗ ( x ) + δ p 1 ( x ) v + δ p 2 ( x ) g ) \begin{aligned} & \min _{u}\left\|u-u_{\text {norm}}\right\|^{2} \\ & \text { s.t. }\left(\delta p_{2}(x) k\right) u \leq\left(V^{*}(x)+\delta p_{1}(x) v+\delta p_{2}(x) g\right) \end{aligned} u min ∥ u − u norm ∥ 2 s.t. ( δ p 2 ( x ) k ) u ≤ ( V ∗ ( x ) + δ p 1 ( x ) v + δ p 2 ( x ) g ) Example: Planar Vehicle f ( x ) = [ v cos θ v sin θ ω ] = [ v cos θ v sin θ 0 ] + [ 0 0 1 ] ω A = δ p 3 ( x ) b = V ∗ ( x ) + δ p 1 ( x ) v cos θ + δ p 2 ( x ) v sin θ \begin{aligned} f(x) & =\left[\begin{array}{c} v \cos \theta \\ v \sin \theta \\ \omega \end{array}\right]=\left[\begin{array}{c} v \cos \theta \\ v \sin \theta \\ 0 \end{array}\right]+\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right] \omega \\ A & =\delta p_{3}(x) \\ b & =V^{*}(x)+\delta p_{1}(x) v \cos \theta+\delta p_{2}(x) v \sin \theta \end{aligned} f ( x ) A b = ⎣ ⎡ v cos θ v sin θ ω ⎦ ⎤ = ⎣ ⎡ v cos θ v sin θ 0 ⎦ ⎤ + ⎣ ⎡ 0 0 1 ⎦ ⎤ ω = δ p 3 ( x ) = V ∗ ( x ) + δ p 1 ( x ) v cos θ + δ p 2 ( x ) v sin θ Bringing Back Disturbance The above safety filtering mechanisms can also be applied in the presence of uncertainty. Let's first look at the least restrictive controller. There u safe ∗ ( x ) u_{\text{safe}}^{*}(x) u safe ∗ ( x )
u safe ∗ ( x ) = arg max u min d ∂ V ∗ ( x ) ∂ x ⋅ f ( x , u , d ) u_{\text {safe}}^{*}(x)=\argmax_{u} \min _{d} \frac{\partial V^{*}(x)}{\partial x} \cdot f(x, u, d) u safe ∗ ( x ) = u arg max d min ∂ x ∂ V ∗ ( x ) ⋅ f ( x , u , d ) A particularly interesting class of dynamics is control and disturbance affine dynamics:
f ( x , u , d ) = f 1 ( x ) + f 2 ( x ) u + f 3 ( x ) d f\left(x, u, d\right)=f_{1}(x)+f_{2}(x) u+f_{3}(x) d f ( x , u , d ) = f 1 ( x ) + f 2 ( x ) u + f 3 ( x ) d Thus,
u safe ∗ ( x ) = arg max u ∂ V ∗ ( x ) ∂ x ⋅ f 1 ( x ) + ∂ V ∗ ( x ) ∂ x ⋅ f 2 ( x ) u + min d ∂ V ∗ ( x ) ∂ x ⋅ f 3 ( x ) d = arg max u ∂ V ∗ ( x ) ∂ x ⋅ f 2 ( x ) u \begin{aligned} u_{\text {safe}}^{*}(x) & =\argmax_u \frac{\partial V^{*}(x)}{\partial x} \cdot f_{1}(x)+\frac{\partial V^{*}(x)}{\partial x} \cdot f_{2}(x) u +\min _{d} \frac{\partial V^{*}(x)}{\partial x} \cdot f_{3}(x) d \\ & =\argmax_u \frac{\partial V^{*}(x)}{\partial x} \cdot f_{2}(x) u \end{aligned} u safe ∗ ( x ) = u arg max ∂ x ∂ V ∗ ( x ) ⋅ f 1 ( x ) + ∂ x ∂ V ∗ ( x ) ⋅ f 2 ( x ) u + d min ∂ x ∂ V ∗ ( x ) ⋅ f 3 ( x ) d = u arg max ∂ x ∂ V ∗ ( x ) ⋅ f 2 ( x ) u Thus, the safety control does not directly depend on d d d V ∗ ( x ) V^{*}(x) V ∗ ( x ) ∂ V ∗ ∂ x ( x ) \frac{\partial V^{*}}{\partial x}(x) ∂ x ∂ V ∗ ( x ) d d d
Example z ˙ = v v ˙ = k u + g + d \begin{aligned} & \dot{z}=v \\ & \dot{v}=k u+g+d \end{aligned} z ˙ = v v ˙ = k u + g + d Let − u ˉ ≤ u ≤ u ˉ , − d ˉ ≤ d ≤ d ˉ -\bar{u} \leq u \leq \bar{u},-\bar{d} \leq d \leq \bar{d} − u ˉ ≤ u ≤ u ˉ , − d ˉ ≤ d ≤ d ˉ
Here, x = [ z v ] x=\left[\begin{array}{l}z \\ v\end{array}\right] x = [ z v ] ∂ V ∗ ( x ) ∂ x = [ p 1 ( x ) p 2 ( x ) ] \frac{\partial V^{*}(x)}{\partial x}=\left[\begin{array}{l}p_{1}(x) \\ p_{2}(x)\end{array}\right] ∂ x ∂ V ∗ ( x ) = [ p 1 ( x ) p 2 ( x ) ]
f 1 ( x ) = [ v g ] f 2 ( x ) = [ 0 k ] f 3 ( x ) = [ 0 1 ] f_{1}(x)=\left[\begin{array}{l} v \\ g \end{array}\right] \quad f_{2}(x)=\left[\begin{array}{l} 0 \\ k \end{array}\right] \quad f_{3}(x)=\left[\begin{array}{l} 0 \\ 1 \end{array}\right] f 1 ( x ) = [ v g ] f 2 ( x ) = [ 0 k ] f 3 ( x ) = [ 0 1 ] u safe ∗ ( x ) = arg max u min d [ p 1 ( x ) p 2 ( x ) ] ( [ v g ] + [ 0 k ] u + [ 0 1 ] d ) = arg max u [ p 1 ( x ) p 2 ( x ) ] [ 0 k ] u = arg max u ( p 2 ( x ) k ) u = { u ˉ if p 2 ( x ) ⩾ 0 − u ˉ otherwise \begin{aligned} u_{\text {safe}}^{*}(x)& =\argmax_u \min _{d}\left[\begin{array}{ll} p_{1}(x) & p_{2}(x) \end{array}\right]\left(\left[\begin{array}{l} v \\ g \end{array}\right]+\left[\begin{array}{l} 0 \\ k \end{array}\right] u+\left[\begin{array}{l} 0 \\ 1 \end{array}\right] d\right) \\ & =\argmax_u \left[\begin{array}{ll} p_{1}(x) & p_{2}(x) \end{array}\right]\left[\begin{array}{l} 0 \\ k \end{array}\right] u \\ & =\argmax_u \left(p_{2}(x) k\right) u \\ & = \begin{cases}\bar{u} & \text { if } \; p_2(x) \geqslant 0 \\ -\bar{u} & \text{ otherwise }\end{cases} \end{aligned} u safe ∗ ( x ) = u arg max d min [ p 1 ( x ) p 2 ( x ) ] ( [ v g ] + [ 0 k ] u + [ 0 1 ] d ) = u arg max [ p 1 ( x ) p 2 ( x ) ] [ 0 k ] u = u arg max ( p 2 ( x ) k ) u = { u ˉ − u ˉ if p 2 ( x ) ⩾ 0 otherwise A similar analysis can be done for the planar vehicle. QP-based Safety Filter Now, let's move on to the QP-based safety filter. Once again we want to pick a control input among the set of safe controls that is closest to u norm u_{\text {norm}} u norm
u x ( x ) = arg min ∥ u − u norm ∥ 2 2 s.t. u is safe \begin{aligned} u^{x}(x)=&\arg \min \left\|u-u_{\text {norm}}\right\|_{2}^{2} \\ & \text{s.t. } u \text { is safe } \end{aligned} u x ( x ) = arg min ∥ u − u norm ∥ 2 2 s.t. u is safe u is safe ≡ min d V ∗ ( x ( t + δ ) ) ⩾ 0 ← even under the worst-case disturbance, the next state is outside the BRT \begin{array}{r} u \text { is safe } \equiv \min_d V^{*}(x(t+\delta)) \geqslant 0 \leftarrow \text { even under the worst-case } \\ \text { disturbance, the next state } \\ \text { is outside the BRT } \end{array} u is safe ≡ min d V ∗ ( x ( t + δ )) ⩾ 0 ← even under the worst-case disturbance, the next state is outside the BRT V ∗ ( x ( t + δ ) ) = V ∗ ( x ) + δ ∂ V ∗ ∂ x ⋅ f ( x , u , d ) = V ∗ ( x ) + δ ∂ V ∗ ∂ x ⋅ f 1 ( x ) + δ ∂ V ∗ ∂ x ⋅ f 3 ( x ) d + δ ∂ V x ∂ x f 2 ( x ) u min d V ∗ ( x ( t + δ ) ) = ( V ∗ ( x ) + δ ∂ V ∗ ∂ x ⋅ f 1 ( x ) ) + min d δ ∂ V ∗ ∂ x ⋅ f 3 ( x ) d + δ ∂ V ∗ ∂ x ⋅ f 2 ( x ) u = ( V ∗ ( x ) + δ ∂ V ∗ ∂ x ⋅ f 1 ( x ) ) + δ ∂ V ∗ ∂ x ⋅ f 3 ( x ) d ∗ + δ ∂ V ∗ ∂ x ⋅ f 2 ( x ) u \begin{aligned} V^{*}(x(t+\delta))&=V^{*}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f\left(x, u, d\right) \\ & =V^{*}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{1}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{3}(x) d+\delta \frac{\partial V^{x}}{\partial x} f_{2}(x) u \\ \min_d V^{*}(x(t+\delta))&=\left(V^{*}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{1}(x)\right)+\min _{d} \delta \frac{\partial V^{*}}{\partial x} \cdot f_{3}(x) d +\delta \frac{\partial V^{*}}{\partial x} \cdot f_{2}(x) u \\ & =\left(V^{*}(x)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{1}(x)\right)+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{3}(x) d^{*}+\delta \frac{\partial V^{*}}{\partial x} \cdot f_{2}(x) u \end{aligned} V ∗ ( x ( t + δ )) d min V ∗ ( x ( t + δ )) = V ∗ ( x ) + δ ∂ x ∂ V ∗ ⋅ f ( x , u , d ) = V ∗ ( x ) + δ ∂ x ∂ V ∗ ⋅ f 1 ( x ) + δ ∂ x ∂ V ∗ ⋅ f 3 ( x ) d + δ ∂ x ∂ V x f 2 ( x ) u = ( V ∗ ( x ) + δ ∂ x ∂ V ∗ ⋅ f 1 ( x ) ) + d min δ ∂ x ∂ V ∗ ⋅ f 3 ( x ) d + δ ∂ x ∂ V ∗ ⋅ f 2 ( x ) u = ( V ∗ ( x ) + δ ∂ x ∂ V ∗ ⋅ f 1 ( x ) ) + δ ∂ x ∂ V ∗ ⋅ f 3 ( x ) d ∗ + δ ∂ x ∂ V ∗ ⋅ f 2 ( x ) u Where d ∗ = arg min d ∂ V ∗ ∂ x ⋅ f 3 ( x ) d d^*=\argmin_d \frac{\partial V^*}{\partial x} \cdot f_3(x) d d ∗ = arg min d ∂ x ∂ V ∗ ⋅ f 3 ( x ) d d ∗ d^* d ∗
Again, we have a constraint of form A u + b ⩾ 0 A u+b \geqslant 0 A u + b ⩾ 0 δ ⋅ ∂ V ∗ ∂ x ⋅ f 3 ( x ) d ∗ \delta \cdot \frac{\partial V^{*}}{\partial x} \cdot f_{3}(x) d^{*} δ ⋅ ∂ x ∂ V ∗ ⋅ f 3 ( x ) d ∗ b b b
Example: Quadrotor Again ∂ V ∗ ( x ) ∂ x ⋅ f 1 ( x ) = v p 1 ( x ) + g p 2 ( x ) \frac{\partial V^{*}(x)}{\partial x} \cdot f_{1}(x)=v p_{1}(x)+g p_{2}(x) ∂ x ∂ V ∗ ( x ) ⋅ f 1 ( x ) = v p 1 ( x ) + g p 2 ( x ) d ∗ = arg min d ∂ V ∗ ( x ) ∂ x ⋅ f 3 ( x ) d = arg min d p 2 ( x ) d = { − d ˉ if p 2 ( x ) ⩾ 0 d ˉ if p 2 ( x ) < 0 \begin{aligned} d^{*}&=\argmin_d \frac{\partial V^{*}(x)}{\partial x} \cdot f_{3}(x) d \\ & =\argmin _{d} p_{2}(x) d \\ & =\left\{\begin{array}{l} -\bar{d} \quad \text { if } \; p_{2}(x) \geqslant 0 \\ \bar{d} \quad \text { if } \; p_{2}(x)<0 \end{array}\right. \end{aligned} d ∗ = d arg min ∂ x ∂ V ∗ ( x ) ⋅ f 3 ( x ) d = d arg min p 2 ( x ) d = { − d ˉ if p 2 ( x ) ⩾ 0 d ˉ if p 2 ( x ) < 0 Thus, ∂ V ∗ ( x ) ∂ x ⋅ f 3 ( x ) d ∗ = p 2 ( x ) d ∗ = { − p 2 ( x ) d ˉ if p 2 ( x ) ⩾ 0 p 2 ( x ) d ˉ if p 2 ( x ) < 0 = ∣ p 2 ( x ) ∣ d ˉ \frac{\partial V^{*}(x)}{\partial x} \cdot f_{3}(x) d^{*}=p_{2}(x) d^{*}= \begin{cases}-p_{2}(x) \bar{d} & \text { if } p_{2}(x) \geqslant 0 \\ p_{2}(x) \bar{d} & \text { if } p_{2}(x)<0\end{cases}=\left|p_{2}(x)\right| \bar{d} ∂ x ∂ V ∗ ( x ) ⋅ f 3 ( x ) d ∗ = p 2 ( x ) d ∗ = { − p 2 ( x ) d ˉ p 2 ( x ) d ˉ if p 2 ( x ) ⩾ 0 if p 2 ( x ) < 0 = ∣ p 2 ( x ) ∣ d ˉ
∂ V ∗ ( x ) ∂ x ⋅ f 2 ( x ) = p 2 ( x ) k \frac{\partial V^{*}(x)}{\partial x} \cdot f_{2}(x)=p_{2}(x) k ∂ x ∂ V ∗ ( x ) ⋅ f 2 ( x ) = p 2 ( x ) k Thus, the linear constraint is given by:
b = V ∗ ( x ) + δ V p 1 ( x ) + δ g p 2 ( x ) + δ ∣ p 2 ( x ) ∣ d ˉ A = δ p 2 ( x ) k A u + b ⩾ 0 \begin{aligned} & b=V^{*}(x)+\delta V p_{1}(x)+\delta g p_{2}(x)+\delta\left|p_{2}(x)\right| \bar{d} \\ & A=\delta p_{2}(x) k \\ & A u+b \geqslant 0 \end{aligned} b = V ∗ ( x ) + δ V p 1 ( x ) + δ g p 2 ( x ) + δ ∣ p 2 ( x ) ∣ d ˉ A = δ p 2 ( x ) k A u + b ⩾ 0 Planar Vehicle Example f ( x , u , d ) = [ v cos θ + d x v sin θ + d y ω ] where ∣ ω ∣ ≤ ω ˉ ← control, ∥ d x d y ∥ ≤ d ˉ ← Disturbance f ( x , u , d ) = [ v cos θ v sin θ 0 ] + [ 0 0 1 ] ω + [ 1 0 0 1 0 0 ] ( d x d y ) ← 2D disturbance \begin{gathered} f(x, u, d)=\left[\begin{array}{c} v \cos \theta+d_x \\ v \sin \theta+d_y \\ \omega \end{array}\right] \quad \text { where }|\omega| \leq \bar{\omega} \leftarrow \text { control, } \left\| \begin{array}{c} d_{x} \\ d_y \end{array}\right\| \leq \bar{d} \leftarrow \text { Disturbance } \\ f(x, u, d)=\left[\begin{array}{c} v \cos \theta \\ v \sin \theta \\ 0 \end{array}\right]+\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right] \omega+\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right]\left(\begin{array}{c} d x \\ d y \end{array}\right) \leftarrow \text { 2D disturbance } \end{gathered} f ( x , u , d ) = ⎣ ⎡ v cos θ + d x v sin θ + d y ω ⎦ ⎤ where ∣ ω ∣ ≤ ω ˉ ← control, ∥ ∥ d x d y ∥ ∥ ≤ d ˉ ← Disturbance f ( x , u , d ) = ⎣ ⎡ v cos θ v sin θ 0 ⎦ ⎤ + ⎣ ⎡ 0 0 1 ⎦ ⎤ ω + ⎣ ⎡ 1 0 0 0 1 0 ⎦ ⎤ ( d x d y ) ← 2D disturbance Safety Filtering Pros and Cons Pros A very practical way to ensure safety on top of any nominal and potentially unsafe policy, including learning-based policies.
Cons Only greedily optimize for performance. Doesn't take future policy or performance into account. It can lead to suboptimal performance in the future.